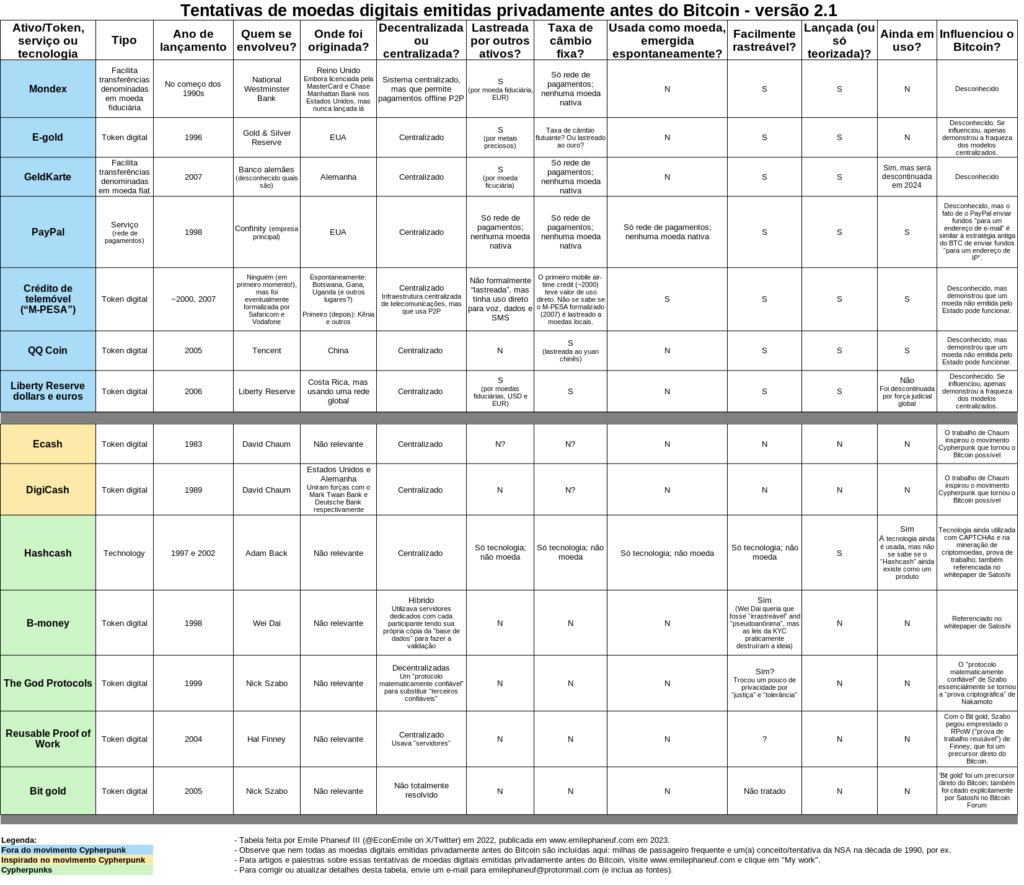
For the past several years I have studied the evolution of ideas that eventually resulted in the launch of Bitcoin in 2009. This study encompasses two main areas. The first area covers privately-issued digital currencies before Bitcoin (the step-by-step evolution of thought about how to make a decentralized and robust cryptocurrency work in the first place). The second area covers Bitcoin’s economic and philosophical origins to explore what motivated cryptographers, mathematicians, etc. to develop privately-issued currency.
This personal inquiry has led me to do a fair bit of writing and presenting over the years (see here, here, here, and here, for example). But to understand how governance without government could be possible (relevant to understanding Bitcoin’s own decentralized governance model), I also found myself studying the work of David Friedman, as well as often less understood societies such as that of 18th century pirates and American prison gangs, ultra-Orthodox Jewish diamond traders, Dark Net markets, informal markets more generally, and a lot more. The rabbit hole never ends.
At a conference and later as part of a podcast, I presented a table that I had built in order to keep track of some of the attempts, successful and unsuccessful, to launch a privately-issued digital currency. Each time, audience members expressed their liking of it and requested that I share it. So here it is: version 2.0. Enjoy.
Feel free to share widely. I release it under Creative Commons Attribution 4.0 International License and request a link back here, which also gives anyone you share it with the opportunity to see updates that I may make to it over time.
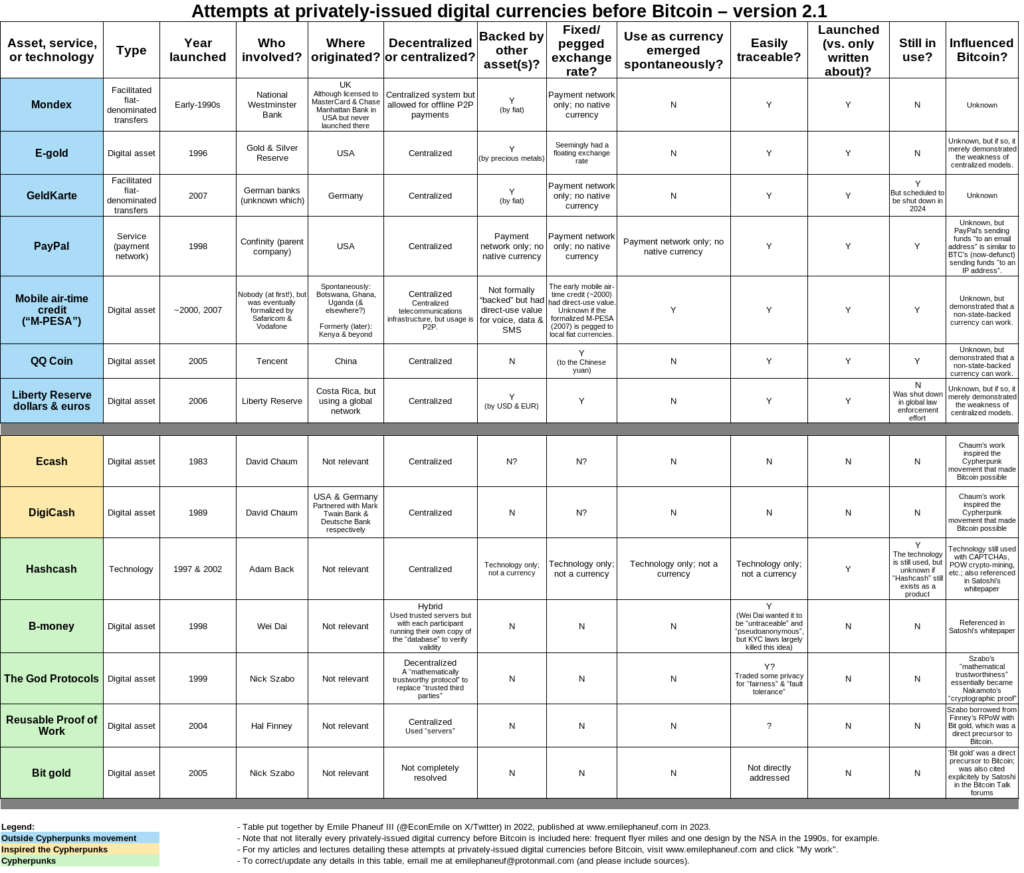
E para os falantes de português, tem uma versão da mesma tabela aqui para você também: